Generating Fractals Based on Spatial Organizations
Magdy M. Ibrahim and Robert J. Krawczyk
Illinois Institute of Technology
College of Architecture, Chicago, IL USA
- Abstract
- 1. Introduction
- 2. Creating a fractal
- 3. Shape of generators and initiators
- 4. Direction and proportion
- 5. The meaning of the generator
- 6. Observations
- References
This paper investigates an approach to the use of fractals in architectural design. Two major aspects are discussed. First, the effect of the direction of the line segments on the generated fractal, as well as, the proportions between the generator and the initiator. Secondly, the meanings attached to the lines segments that constitute the fractal are based on some known architectural organization. The goal is to develop a basis for using fractals to suggest architectural forms.
A fractal is an object or quantity that displays self-similarity on all scales. The object need not exhibit exactly the same structure at all scales, but the same пїЅtypeпїЅ of structures must appear on all scales (Weisstein 1999). Fractals were first discussed by Mandelbrot (Mandelbrot 1978) but the idea was identified as early as 1925. Fractals have been investigated for their visual qualities as art, their relationship to explain natural processes, music, medicine, and in mathematics (Pickover 1996).
Examining fractals, we were able to classify them into two major categories depending on the way they are created, and the mathematical method used to calculate them. From the drawing method point of view, the first is line or vector fractals. These are generated from the replacement of a group of vectors, such like the Dragon Curve, as in Figure 1a. The second are fractals that are generated as a group of points in the complex plane, such as the Mandelbrot set and the Julia set, as in Figure 1b.
From the mathematical point of view, we can classify fractals into three major categories. The first, IFS, iterated function system, like Koch Snowflake, Cantor set, Barnsley's Fern and the Dragon Curve. This method can generate a fractal from any set of vectors or any defined curve. The second is the complex number fractals. They can be two-dimensional of three-dimensional or multiple-dimensional. They represent a single case of the IFS that is using the complex numbers or the hyper complex numbers in a Cartesian plane to plot the fractals. The Mandelbrot set and Julia set are examples of these. The third is orbit fractals. They are generated by plotting an orbit path in two or three-dimensional space. Examples include the Bifurcation orbit, Lorenz Attractors, Rossler Attractors, Henon Attractors, Pickover Attractors, Gingerbreadman, and Martin Attractors. these are associated with the chaos theory.

Fig. 1. Types of fractals.
In this research, we are interested in the vector-based fractals and the use of the replacement concept and the iterated function system as a way to generate them. These fractals have directional and geometrical properties that make them possibility suitable for applications in architecture. Vector-based fractals can be described in terms of vertices and the lines connecting them. This has the potential to be used directly as architectural elements or to simply use the vertices to define the locations of such elements.
Chris Yessios with Peter Eisenman (Yessios 1987) was among the first to write about utilizing fractals and fractal geometry in architecture. Yessios described a way computers can be introduced to architectural design as an explorer and generator of architectural forms. He used the fractal geometry, arabesque ornamentation and DNA/RNA biological processes as fractal generators. A fractal program was developed that enabled him to use several generators on the same base and to go many steps forward in the iteration process, as well as, backward. The project that was used in this investigation was a studio project to design a building for a competition given a specific
architectural program.
More recently, S. Durmisevic and O. Ciftcioglu (Durmisevic and Ciftcioglu 1998) discussed another approach on how fractals can be used in the architectural design. They proposed to use a fractal tree form as an indicator of a road infrastructure and another fractal to determine the type of architectural forms to place along this transportation spine. The fractal geometry was used for architectural forms and urban planning. No other similar studies could be found where fractals were used as architectural form generators to suggest three-dimensional forms. The results from these two suggest that the explicit self-similarity and the repetition of the same shape may distract from developing interesting architectural forms, so both developed means to modify the replication.
A vector-base fractal is composed of two parts: the initiator and the generator. For example, the Koch Snowflake starts with an equilateral triangle as the initiator. The generator is a line that is divided into three equal segments. The middle segment forms an equilateral triangle as in Figure 2.
By replacing every line of the initiator with the full generator, we get the first iteration of the snowflake. By iterating this operation again and again, replacing every line of the new initiator with the full generator, we end with a figure that approximates a snowflake. The iteration process should continue to infinity to generate a real Koch Snowflake fractal, but as we are interested in the evolving form, we only iterate the function for some finite number of times. Figure 3 displays the Koch Snowflake with 3 iterations. If the generator is changed, inverted, we can develop an entirely different form, the Koch Antisnowflake as in Figure 3.
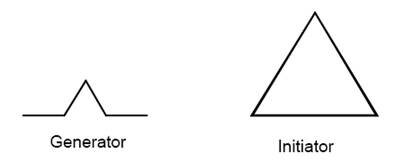
Fig. 2. Generator and initiator.

Fig. 3. The Koch Snowflake and the Antisnowflake.
3. Shape of generators and initiators
There is a group of fractals that have been formally identified, including Mandelbrot set variations as described in his book пїЅThe Fractal Geometry of NatureпїЅ (Mandelbrot 1983) that depend on the concept of replacement. Some of the IFS fractals are: Cantor Set, Barnsley's Fern, Koch Antisnowflake, Koch Snowflake, Box Fractal, Cantor Square Fractal, Cesàro Fractal, Dragon Curve, Gosper Island Fractal, H-Fractal, Sierpinski Curve, Minkowski Sausage. Some of these are displayed in Figure 4.

Fig. 4. Tree fractal, Cesàro fractal, Barnsley's Fern, Dragon Curve, H-fractal, Sierpinski curve, square and triangle.
All of these fractals are based on simple geometric shapes. Shakiban and Berstedt (1998) discussed a new generating procedure based on vector calculus and modular arithmetic to generate the Koch Snowflake. The procedure was then applied to create more generalized snowflakes rather than the triangular classical snowflakes. They also suggested the use of n-sided polygons, such as pentagons as initiators. In all cases the replacements made at each iteration are consistent and unvaried.
In all these fractals, the generator and the initiator have no specific meaning. They are mostly based on simple geometric shapes: lines, squares, or triangles that are able to produce an interesting arrangement. In his book, Mandelbrot mostly used squares in his fractal generation. Mandelbrot was interested in the calculation of the fractal dimension, and as he produced interesting patterns of fractals, he was concerned about the comparison between the fractal dimensions of each generated fractal. Although, as described by Carl Bovill (1996), the fractal dimension has a meaning in evaluating the visual richness or density, for architects it has less meaning in the generation of new forms. These shapes have no real meaning in architecture.
YessiosпїЅs (1987) implementation of fractal generation was highly interactive and allowed a fractal to be developed one iteration at a time or at multiple increments. At the same time, generators could be changed, replaced, deleted, or inserted, at any iteration. The generation process could go forward and backward allowing the designer to return to an earlier state. The fractals resulted in three-dimensional models but no explicit meaning of these generators or initiators was shown. No indication whether they were site boundaries or circulation axes, or any other architectural organizational element. Differing from traditional fractal generation, this approach enabled a designer to interfere with the generated form at any time of the process. This is a major deviation from the basic concept of the fractal generation as an uninterrupted process. As an experimental design tool it does offer a variation not considered by others.
Another interesting method to modify the geometric shapes produced by a fractal comes from the random selection of the direction and displacement of the initiator. Mandelbrot discussed this when he was describing the random Koch coastline, and Brown fractals and the random midpoint displacement curves. Similar application in architectural fractals was not found.
As we started to investigate the selection of the generator and initiator, our initial focus was on the effect of proportion and direction of the initiator on the produced fractal as related to the generator. Normally, the length of the generator is equal to a segment of the initiator and the direction of the line segments in the generator and initiator are the same as seen in the Koch Snowflake in Figure 3.
One possible variation is to modify the direction of the entire generator or initiator or individual parts of each and the orientation of the generator as it is placed on the initiator. Figure 5 displays the Koch Snowflake with the generator in one direction and normal and reversed direction for the initiator. When the initiator is reversed the Antisnowflake appears. Figure 6 reverses the direction of the placement of the generator. The fractals developed starting at the second iteration are undocumented versions of the Koch Snowflake. Additional variations were found by modifying the direction of individual line segments within the generator or the initiator.
In addition to direction, the proportions of the line segments in the generator were modified in relationship to the initiator. To demonstrate this concept, we used a square initiator and the normal Koch Snowflake generator. Figure 7 shows fractals that are based on generators that range from 25% to 75% of the size of the initiator.

Fig. 5. The direction effect on the generated fractal applied on the simple Koch Snowflake.

Fig. 6. The effect of the direction of the placement of the generator on the generated fractal applied on the simple Koch Snowflake.

Fig. 7. The proportion effect on the generated fractal applied on the simple square.
5. The meaning of the generator
As previously noted, the classical fractals have no specific meaning associated to their shapes; they are simply forms that generate interesting fractals. Selecting the generator can be based on architectural organizational schemes used as major axes of a site planning or a building, or using the patterns discussed by Francis D.K. Ching (1979) in organizing spaces.
Another approach to develop a generator is to use studies such as DurandпїЅs. In the book пїЅPrпїЅcis des lecons dпїЅarchitectureпїЅ, Jean L. Durand (1802) describes a compendium of neo-classical design rules. Cross axes, grids, squares and circles are taken as primitive shapes. He demonstrates, by diagrams, how to assemble these, into symmetrical skeletons of construction lines, Figure 8. DurandпїЅs rules do not provide a complete, consistent specification of a classical architectural language, but are a straightforward method to develop them into a grammar that does.
We selected some of these diagrams and defined them as the initiator for the generation of fractals based on the Koch Snowflake. The goal was to investigate if the fractal generated from them might then be related to a rational organizational pattern.

Fig. 8. Durand neo-classical design rules.
In addition to these initiators, we also applied the proportion and the direction studies to them. The created fractals now are determined by two factors: the proportion of the generator to the initiator, and the direction of the vectors of the generator. Figure 9 displays a series based on these parameters.
It was observed that some of the shapes have changed after several iterations into some different organizations. The square with two horizontal compartments was converted into a three compartments shape rather than two. And other shape that had a vertical axis was converted into a shape that have horizontal axis of symmetry. These generators have different vector directions, starting from all vectors right to all vectors left.
Fractals have a great visual richness, but despite that, they cannot contribute to the simulation of architecture forms unless they can have meaning associated to the components used. The concept of utilizing the fractals, as a form investigating technique can be useful if they are rationalized so that they relate to architectural elements like axes or masses, some architecturally related organizational scheme.
There are more than the regular fractals that can be produced with the same iteration concept. Investigating the directional effect of the generator can lead to some unidentified fractals with different visual characteristics, as well as, the change in the proportions of the generator and the initiator. These variations indicate a possible approach for architectural form development.
Continued research will focus on possible meanings of the initiator and methods of transforming these fractals into three-dimensions.

Fig. 9. DurandпїЅs design rules with the different generators applied to them.
Bovill C. (1996). Fractals in architecture and design. Boston: BirkhпїЅuser.
Ching, Francis D.K. (1979). Architecture: Form, Space and Order. New York: Van Nostrand Reinhold Company.
Durand, J. (1802). PrпїЅcis des Lecons dпїЅArchitecture.
Durmisevic, S. and O. Ciftcioglu. (1998). Fractals in Architectural Design. In Mathematics and Design. (1998) Javier Barrallo the university of the Basque Country
Mandelbrot, Benoit B. (1982). The Fractal Geometry of Nature. San Francisco: W.H. Freeman.
Mitchell, William. (1990). The Logic of Architecture: Design, Computation and Cognition. Cambridge, Massachusetts: MIT Press.
Pickover, Clifford. (1996). Fractal horizons. New York: St. MartinпїЅs Press.
Shakiban C. and Berstedt J.E. (1998) Generalized Koch Snowflakes. In Bridges Mathematical Connections in Art, Music and Science.
Weisstein, Eric W. (1999) Concise Encyclopedia of Mathematics, CD-ROM edition 1.0, Chapman & Hall/CRCnetBASE
Yessios, Chris I. (1987). A Fractal Studio. In ACADIA пїЅ87 Workshop Proceedings.