Topology-Driven Progressive Mesh Construction for Hardware-Accelerated Rendering

Pavlo Turchyn
Department of Mathematical Information Technology,
University of Jyväskylä, Finland
pturchy@cc.jyu.fi

Sergey Korotov
Department of Mathematical Information Technology,
University of Jyväskylä, Finland
korotov@mit.jyu.fi

Contents

· Abstract

· 1. Introduction

· 2. Previous Work

· 3. Topology-driven progressive mesh construction

· 3.1. Patch coverage problem

· 3.2. Optimization for vertex cache

· 3.3. Progressive mesh construction

· 4. Numerical results

· 5. Conclusions

· References

Abstract: We present an algorithm for a construction of progressive meshes, which are used for rendering from static memory buffers. Compared to the previous work our scheme reduces memory consumption while maintaining a good vertex cache coherency.

Keywords: continuous level-of-detail, view-independent progressive mesh, hardware vertex processing, vertex cache, sliding window

1. Introduction

Progressive meshes scheme, which is also referred as continuos level-of-detail scheme, encodes a sequence of meshes with different geometrical complexity [8]. Originally, algorithm suggests updating memory buffers, which contain mesh's geometry (vertex buffer) and connectivity information (index buffer). Updates of vertex buffer may be avoided by using corresponding simplification operator (e.g. half-edge collapse [10]) at the expense of some geometric error increase. Sliding window algorithm [6] may be used to avoid updates of the index buffer at the expense of a large resulting index buffer size. The latter algorithm is optimal in sense of memory management in major 3D APIs (e.g. Microsoft Direct3D) since changing memory buffers, which are located in GPU-accessible memory, imposes CPU overhead and needs additional memory to avoid breaking CPU-GPU parallelism. Moreover, instancing does not require any additional memory.

Since the introduction of FIFO cache for post-processed vertices in [9], it has been widely implemented in the commodity hardware. As the complexity of per-vertex computations grows, the vertex processing performance improvements focused on cache miss rate. Although vertex cache is transparent to the application, a care must be taken to avoid its trashing. [1] presents a smart update algorithm for progressive meshes that preserves original optimized rendering order. The idea of preserving original order is also exposed in skip-strips scheme [4], which also relies on the hardware's ability to detect degenerate triangles efficiently. However, such schemes still require updating index buffer.

Our algorithm uses sliding window scheme for rendering of the progressive mesh, while trying to minimize size of the data used by the algorithm. Also, we show that when optimization for vertex cache is incorporated as one of the objectives into the simplification process, the resulting cache coherency is identical to the one that is obtained using dedicated vertex-cache optimizers like NVTriStrip [11].

2. Previous work

Mesh M is a set of vertices and a set of indices, which define vertices connectivity. We seek to construct such sequence {r₁,..r_n} of parameters for simplification operator S, where each r_i minimizes simplification metric E [10]

.

Throughout this paper we use vertex removal or half-edge collapse simplification operator.

We call a set of triangles in 1-ring neighborhood of the vertex a patch. The latter vertex is called the center of patch. [6] describes sliding window algorithm. Assume that we have a mesh on which a list P={p₁,...,p_n} of non-overlapping patches is defined. The index buffer I is initialized with the indices of P. Progressive mesh construction algorithm iteratively takes patch from the top of the list, apply simplification operator and then appends resulting triangulation to the end of index buffer.

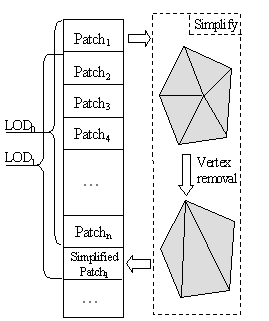
Fig. 1. Index buffer in sliding window algorithm

In such scheme the mesh with the required LOD can be rendered simply by choosing appropriate window in the index buffer. When all patches in the list P are simplified, one has to perform a next pass (restart algorithm) and build new P from the simplified mesh. Then new P is processed in the same manner.

Advantages of the sliding window scheme include:

- No additional memory is required for mesh instancing. Because memory buffers are static, they are shared among all mesh instances. This allows extensive use of mesh instancing in application.

- Low overhead due to the LOD switching. Because memory buffers are remaining static, no CPU overhead occurs due to locking or copying data; no additional memory is required for rename buffers, which hold data still being processed by GPU.

- Efficient progressive transmission (visualization of geometry before the entire file is received). The data, which is needed for more detailed mesh, is appended to index and vertex buffers, thus memory is updated locally and sequentially.

- Efficient geomorphing. Geometry, which is affected by LOD switching, is located exactly at the beginning/end of the LOD window, and thus it can be easily rendered separately from the geometry that does not require morphing.

The major problem of the algorithm is a size of the index buffer, since approximately 4/6 of indices have to be duplicated each time simplification operator is applied. Also when additional pass occurs we have to rearrange simplified mesh M_i into a new collection of patches, which essentially duplicates indices of M_i.

3. Topology-driven progressive mesh construction

Mesh simplification process is guided by the simplification metric E, which typically accounts for geometric and attributes error. However, when constructing a feasible progressive mesh for sliding window algorithm, we have to follow additional objectives, which take into account only connectivity of the mesh:

- Minimize size of the resulting index buffer I. This factor mainly depends on the number of passes we perform, which in turn depends on how many collapses we perform each pass. In order to maximize the number of collapses we have to maximize the size of P.

- Maximize vertex cache coherency during rendering. This may be done by rearranging patches such that cached vertices are reused among patches.

In our work we follow only these objectives, thus trading off geometric error for the algorithm’s efficiency in terms of index buffer size and vertex cache utilization.

3.1. Patch coverage problem

First, we present a greedy algorithm to find P of maximal size. Assume that we have a mesh with initially unmarked vertices. When we choose a patch, we mark all patches' vertices. Note that any marked vertex cannot be the center of patch since patches cannot overlap. Thus, the strategy of a greedy algorithm is to choose a patch, which introduces the least amount of new marked vertices, since this will leave the biggest number of unmarked vertices that potentially can be patch centers. This strategy can be formulated as finding minimum of the following heuristic

(1)

The problem of building optimal P is a maximum clique problem [13] on a graph, which complements vertices connectivity graph. This problem is NP-complete. We compared performance of the greedy algorithm with heuristic (1) and QUALEX-MS package, which is based on Motzkin-Straus quadratic programming formulation with the complexity O(n³) [2].

Data	Triangles	Patches found
		QUALEX	Greedy
Venus10	6718	1015	984
Venus	67170	9891	9739
Bunny	69451	10316	10301

Table 1. Performance comparison between QUALEX-MS and the greedy algorithm

Two algorithms demonstrate nearly identical performance. On the other hand, greedy search took several seconds, while QUALEX required up to several minutes to perform its first iteration.

3.2. Optimization for vertex cache

Building optimal sequence of triangle strips is NP-hard [5]. The proof that building optimal sequence of patches is of the same complexity follows from the fact that its goals are identical: sharing maximal number of vertices between the subsequent patches and minimizing the number of discontinuities in the sequence. We define the heuristic for a greedy construction of such sequence. Each iteration algorithm looks for a patch that minimizes functional

(2)

Such procedure chooses a patch that introduces the least amount of cache trashing. The convenience of greedy solution is that (2) can be easily incorporated into the functional E. The alternative approach is to construct universal rendering sequence using recursive cut or minimum linear arrangement algorithms [1]. However, average cache miss rate per triangle (ACMR) demonstrated by all these methods is identical in many cases. ACMR is defined as a ratio of the number of cache misses to the number of rendered triangles. , where k is the size of vertex cache.

3.3. Progressive mesh construction

Both (1) and (2) are easily incorporated into the simplification metric E using weighting method. However, since patch coverage problem is more important for practical use, it is advantageous to optimize for this criterion first, and then for the vertex cache. This simplification algorithm is presented in Figure 2.

function BuildProgressiveMesh (Mesh M)

while M.Size>0

List<Patch> P=FindPatches(M);

while P.Size>0

Patch p=GetPatch(P);

P.Remove(p);

If IsSimplificationValid(p) then

Simplify(p); // simplify M

Fig. 2. Progressive mesh construction algorithm

FindPatches builds a list of patches using greedy search as described in Section 3.1. GetPatch returns a patch, which minimizes (2). IsSimplificationValid determines if simplification of the patch results into some undesired effects, e.g. face flipping in half-edge collapse operator. Choosing good criteria for IsSimplificationValid is required in order to avoid destruction of important geometric features.

4. Numerical results

In our numerical experiments we compared our method with two alternative approaches of LOD construction, which also offer advantages of static memory buffers. First approach is discrete LOD (DLOD) where each level is created using quadratic error metric (QEM)-based simplification algorithm with sharp features preservation [7], and then optimized using NVTriStrip library. The other approach is directly taken from [6]. It is QEM-guided construction of view-independent progressive mesh (VIPM) for sliding window algorithm. We used vertex contraction operator for DLOD construction. For both VIPM and topology-driven progressive mesh (TD-VIPM) algorithms we used half-edge collapse operator. We used IsSimplificationValid criteria that only reject face flipping.

There are triangles, which do not participate in the simplification process (i.e. they are not included into the list P by FindPatches procedure), but they are still required in order to render mesh completely using VIPM or TD-VIPM algorithm. Our implementation attaches every such triangle to the patch that shares the most vertices with it.

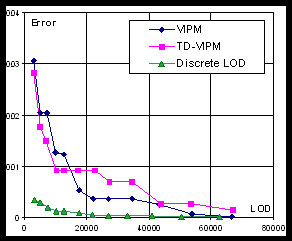
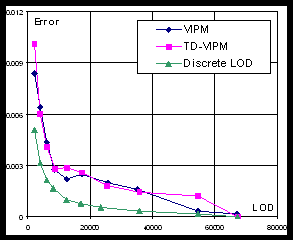
Geometric error. Figure 3 shows geometric error (Hausdorff distance from the original mesh to simplified mesh) of different LODs. Measurements were done using Metro tool [3].

a) Error of Bunny model	b) Error of Venus model

Fig. 3. Geometric error (Hausdorff distance)

Expectedly, the best results are demonstrated by DLOD algorithm since it is using unconstrained geometry-guided simplification. VIPM is only marginally better than TD-VIPM. The explanation of this fact is that we kept the size of index buffer as small as possible by trying not to start new pass until it is absolutely required. However, the size of resulting index buffer in case of VIPM algorithm is still larger than the one in case of TD-VIPM (see Table 2).

Data	Triangles	Index buffer size
		TD-VIPM	VIPM
Bunny	69451	550%	656%
Venus	67170	556%	655%
Hugo	16374	510%	560%
Horse	39698	555%	647%

Table 2. Static index buffer size in % of index buffer of the original model

Visual comparison revealed relatively small differences between algorithms on our datasets. We was able to point out such differences clearly in a limited number of cases. Some of them are shown in Figure 4.

69451 triangles	402 triangles	402 triangles	402 triangles
39698 triangles	560 triangles	560 triangles	560 triangles

Fig. 4. Geometric error a) unsimplified mesh, b) DLOD, c) VIPM, d) TD-VIPM

Index buffer size. Since the index buffer is relatively large, it is advantageous to use a compact representation for connectivity information, such as triangle strips or fans. The natural representation of the patch is a triangle fan (see Figure 5).

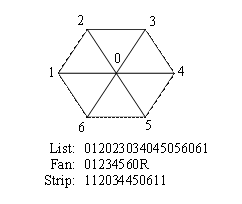
Fig. 5. Different representations of patch connectivity

R is a special index that indicates the end of triangle fan. Additional degenerate triangles are added to the triangle strip in order to render it independently of the preceding indices.

Unfortunately, many GPUs do not handle multiple small triangle fans efficiently. To our knowledge, only optional extension NV_primitive_restart [12] enables efficient processing of such data in OpenGL. This extension is not available on some hardware, so we also consider using common triangle strips for compression. However, since patches are required to be disjoint and strips are generally not optimal for describing such kind of topology, the amount of degenerate triangles is considerable. This result into a modest efficiency of the latter compression scheme (see Table 3).

Data	Triangle fans	Triangle strips
	Compression ratio	Compression ratio	Degenerate triangles
Bunny	0.634	0.835	60.1%
Venus	0.647	0.849	60.8%
Hugo	0.635	0.841	60.4%
Horse	0.646	0.847	60.7%

Table 3. Index buffer compression

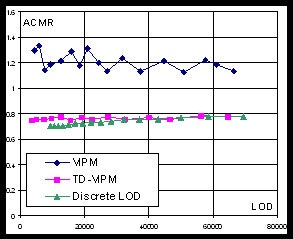
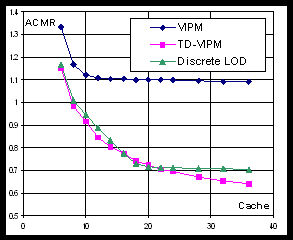
Vertex cache coherency. In terms of vertex cache coherency, VIPM method demonstrates relatively poor performance with ACMR that is close to 1.2 (see Figure 6a). Both TD-VIPM and DLOD algorithms show nearly identical performance in the region of 10-20 cache entries (see Figure 6b).

a) Dependency on LOD (cache size 16)	b) Dependency on cache size (50% LOD)

Fig. 6. ACMR of Bunny model

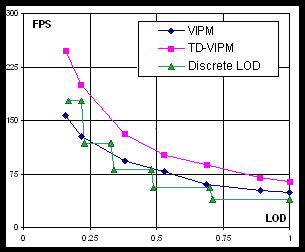
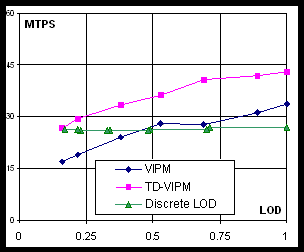
Performance in applications. TD-VIPM and DLOD approaches demonstrate similar performance in terms of ACMR. Although ACMR is the major indicator of achievable speed of geometry processing, some applications may employ specific features of progressive meshes, e.g. efficient geomorphing (see Section 2). We tested an application that performs geomorphing via linear interpolation of two three-component vectors (vertex position and normal). We simulated scenario when camera moves with constant speed toward the object (Venus mesh), and LOD selection function depends on the distance between object and camera linearly. Approximately two thousand triangles are added due to increasing LOD each second.

a) Application speed in frames per second	b) Triangles processing speed in millions triangles per second

Fig. 7. Performance of geomorphing on NVIDIA GeForce FX 5600Go

Both VIPM and TD-VIPM schemes have an advantage over DLOD (see Figure 7) since they allow rendering a part of geometry, which is unaffected by LOD switching, without morphing, thus saving both memory bandwidth and GPU computational resources.

5. Conclusions

Topology-driven method demonstrates significantly better performance than geometry-driven one when size of used data (index buffers) is of the same order. On the other hand, DLOD offers somewhat better visual appearance while TD-VIPM offers progressive transmission and more efficient geomorphing.

Simplification based solely on the topology is naturally suitable for animated meshes, where exact geometry is unknown a priori. Although geometric error is mostly ignored in our scheme, the numerical experiments show that simplification results are still acceptable, particularly for meshes without a big number of sharp features. Because of the good vertex cache coherency and static nature of involved memory buffers, our scheme is aimed at real-time applications, such as video games, architectural walkthrough systems etc, where precise load-balancing or other features, which are offered by progressive meshes, are important in order to maintain interactive frame rates.

Acknowledgements

Horse and Venus models are courtesy of Cyberware, Bunny model is courtesy of Stanford University, Hugo model is courtesy of Laurence Boissieux ©INRIA 2003. This work is partially supported by COMAS Graduate School and Academy of Finland Research Fellowship 208628.

References

[1] Bogomjakov, A., and Gotsman. C. Universal rendering sequences for transparent vertex caching of progressive meshes. In Proceedings of Graphics Interface 2001, B. Watson and J. W. Buchanan, Eds., 2001. pp. 81—90

[2] Busygin, S. A new trust region technique for the maximum weight clique problem. Submitted to Special Issue of Applied Discrete Mathematics: Combinatorial Optimization, 2002. Available at http://www.busygin.dp.ua/npc.html

[3] Cignoni, P., Rocchini, C., and Scopigno, R. Measuring error on simplified surfaces. Computer Graphics Forum 17(2), 1998. pp. 167–174.

[4] El-Sana, J., Azanli, E., and Varshney, A. Skip strips: maintaining triangle strips for view-dependent rendering. In Proceedings of the conference on Visualization '99, IEEE Computer Society Press, 1999. pp. 131–138.

[5] Evans, F., Skiena, S., and Varshney, A. Completing sequential triangulations is hard. Technical Report Department of Computer Science, State University of New York, Stony Brook, 1996.

[6] Forsyth, T. Comparison of VIPM methods. Game Programming Gems 2, M. DeLoura, Ed., Charles River Media, 2001. pp. 363–376.

[7] Garland, M., and Heckbert, P. S. Simplifying surfaces with color and texture using quadric error metrics. In IEEE Visualization '98, D. Ebert, H. Hagen, and H. Rushmeier, Eds., 1998. pp. 263–270.

[8] Hoppe, H. Progressive meshes. In Computer Graphics 30, Annual Conference Series, 1996. pp. 99–108.

[9] Hoppe, H. Optimization of mesh locality for transparent vertex caching. In Proceedings of Siggraph’99, A. Rockwood, Ed., Addison Wesley Longman, Los Angeles, 1999. pp. 269–276.

[10] Luebke, D., Reddy, M., Cohen, J., Varshney, A., Watson, B., and Huebner, R. Level of Detail for 3D Graphics. Computer Graphics and Geometric Modeling. Morgan Kaufmann, 2002.

[11] NVIDIA Corporation. NVTriStrip: a library for vertex cache aware stripification of geometry. Online: http://developer.nvidia.com/object/nvtristrip_library.html

[12] NVIDIA Corporation. NVIDIA OpenGL extension specifications. Online: http://developer.nvidia.com/object/nvidia_opengl_specs.html

[13] Skiena, S. The Algorithm Design Manual. Telos/Springer-Verlag, 1997. pp. 144, 312–314.